Cube root
In mathematics, a cube root of a number, denoted ![\sqrt[3]{x}](/2012-wikipedia_en_all_nopic_01_2012/I/a10c7f2aa138b1565920d17c22062a35.png) or x1/3, is a number a such that a3 = x. All real numbers (except zero) have exactly one real cube root and a pair of complex conjugate roots, and all nonzero complex numbers have three distinct complex cube roots. For example, the real cube root of 8 is 2, because 23 = 8. All the cube roots of −27i are
or x1/3, is a number a such that a3 = x. All real numbers (except zero) have exactly one real cube root and a pair of complex conjugate roots, and all nonzero complex numbers have three distinct complex cube roots. For example, the real cube root of 8 is 2, because 23 = 8. All the cube roots of −27i are
The cube root operation is not associative or distributive with addition or subtraction.
The cube root operation is associative with exponentiation and distributive with multiplication and division if considering only real numbers, but not always if considering complex numbers, for example:
but
Contents |
Formal definition
The cube roots of a number x are the numbers y which satisfy the equation
Real numbers
If x and y are real, then there is a unique solution and so the cube root of a real number is sometimes defined by this equation. If this definition is used, the cube root of a negative number is a negative number.
If x and y are allowed to be complex, then there are three solutions (if x is non-zero) and so x has three cube roots. A real number has one real cube root and two further cube roots which form a complex conjugate pair. This can lead to some interesting results.
For instance, the cube roots of the number one are:
The last two of these roots lead to a relationship between all roots of any real or complex number. If a number is one cube root of any real or complex number, the other two cube roots can be found by multiplying that number by one or the other of the two complex cube roots of one.
Complex numbers
For complex numbers, the principal cube root is usually defined by
where ln(x) is the principal branch of the natural logarithm. If we write x as
where r is a non-negative real number and θ lies in the range
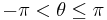 ,
,
then the principal complex cube root is
This means that in polar coordinates, we are taking the cube root of the radius and dividing the polar angle by three in order to define a cube root. With this definition, the principal cube root of a negative number is a complex number, and for instance ![\sqrt[3]{-8}](/2012-wikipedia_en_all_nopic_01_2012/I/e6ca3a3950c92e57c2faf7983423235a.png) will not be
will not be 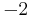 , but rather
, but rather 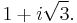
This limitation can easily be avoided if we write the original complex number x in three equivalent forms, namely
The principal complex cube roots of these three forms are then respectively
In general, these three complex numbers are distinct, even though the three representations of x were the same. For example, ∛-8 may then be calculated to be -2, 1 + i√3, or 1 - i√3.
In programs that are aware of the imaginary plane, the graph of the cube root of x on the real plane will not display any output for negative values of x. To also include negative roots, these programs must be explicitly instructed to only use real numbers.
Cube root on standard calculator
From the identity
there is a simple method to compute cube roots using a non-scientific calculator, using only the multiplication and square root buttons, after the number is on the display. No memory is required.
- Press the square root button once. (Note that the last step will take care of this strange start.)
- Press the multiplication button.
- Press the square root button twice.
- Press the multiplication button.
- Press the square root button four times.
- Press the multiplication button.
- Press the square root button eight times.
- Press the multiplication button...
This process continues until the number does not change after pressing the multiplication button because the repeated square root gives 1 (this means that the solution has been figured to as many significant digits as the calculator can handle). Then:
- Press the square root button one last time.
At this point an approximation of the cube root of the original number will be shown in the display.
If the first multiplication is replaced by division, instead of the cube root, the fifth root will be shown on the display.
Why this method works
After raising x to the power in both sides of the above identity, one obtains:
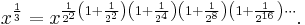 (*)
(*)
The left hand side is the cube root of x.
The steps shown in the method give:
After 2nd step:
After 4th step:
After 6th step:
After 8th step:
etc.
After computing the necessary terms according to the calculator precision, the last square root finds the right hand of (*).
Alternative method
The above method requires the calculator to have a square root button. Having a simple method of calculating the square root the following function converges fast to the result:
Where with each iteration the result comes closer to the cube root of a.
The method requires less iterations than Halley's method but needs more calculations, hidden in determining the square roots. Because of the fast converging an initial approximation of 1 suffices.
Numerical methods
Newton's method is an Iterative method that can be used to calculate the cube root. For real floating point numbers this method reduces to the following iterative algorithm to produce successively better approximations of the cube root of  :
:
The method is simply averaging three factors chosen such that 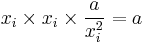 at each iteration.
at each iteration.
Halley's method improves upon this with an algorithm that converges more quickly with each step, albeit consuming more multiplication operations:
With either method a poor initial approximation of 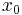 can give very poor algorithm performance, and coming up with a good initial approximation is somewhat of a black art. Some implementations manipulate the exponent bits of the floating point number; i.e. they arrive at an initial approximation by dividing the exponent by 3. This has the disadvantage of requiring knowledge of the internal representation of the floating point number, and therefore a single implementation is not guaranteed to work across all computing platforms.
can give very poor algorithm performance, and coming up with a good initial approximation is somewhat of a black art. Some implementations manipulate the exponent bits of the floating point number; i.e. they arrive at an initial approximation by dividing the exponent by 3. This has the disadvantage of requiring knowledge of the internal representation of the floating point number, and therefore a single implementation is not guaranteed to work across all computing platforms.
Also useful is this generalized continued fraction, based on the nth root method:
If x is a good first approximation to the cube root of z and y = z − x3, then:
The second equation combines each pair of fractions from the first into a single fraction, thus doubling the speed of convergence. The advantage is that x and y are only computed once.
History
In 499 CE Aryabhata, a great mathematician-astronomer from the classical age of Indian mathematics and Indian astronomy, gave a method for finding the cube root of numbers having many digits in the Aryabhatiya (section 2.5).[1]
Approximate values of cube roots of the first 27 natural numbers
See also
- Methods of computing square roots
- List of polynomial topics
- Nth root
- Square root
- Nested radical
- Root of unity
- Shifting nth-root algorithm
References
- ^ Aryabhatiya Marathi: आर्यभटीय, Mohan Apte, Pune, India, Rajhans Publications, 2009, p.62, ISBN 978-81-7434-480-9
![\sqrt[3]{-27i} = \begin{cases} \ \ \ \ \ \ \ \ \ \ \ \ 3i \\ \ \ \frac{3}{2}\sqrt3-\frac{3}{2}i \\ -\frac{3}{2}\sqrt3-\frac{3}{2}i. \end{cases}](/2012-wikipedia_en_all_nopic_01_2012/I/cc057e0da43138bd9820faaeeb23dc79.png)
![(\sqrt[3]{8})^3 = 8](/2012-wikipedia_en_all_nopic_01_2012/I/f19b8a8c1c83acd10b5b2702f95bc113.png)
![\sqrt[3]{8^3} = \begin{cases} \ \ 8 \\ -4%2B4\sqrt{3}i \\ -4-4\sqrt{3}i. \end{cases}](/2012-wikipedia_en_all_nopic_01_2012/I/e4f39ad59519ba52d7001df544992787.png)
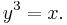
![\sqrt[3]{1} = \begin{cases} \ \ 1 \\ -\frac{1}{2}%2B\frac{1}{2}\sqrt{3}i \\ -\frac{1}{2}-\frac{1}{2}\sqrt{3}i. \end{cases}](/2012-wikipedia_en_all_nopic_01_2012/I/eda747267b015875632f83f730ed5ce9.png)
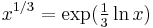
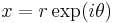
![\sqrt[3]{x} = \sqrt[3]{r}\exp ( \tfrac13 i\theta ).](/2012-wikipedia_en_all_nopic_01_2012/I/01fbda085ddb5fcd1f7db0e9baf0046f.png)
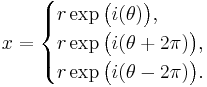
![\sqrt[3]{x} = \begin{cases} \sqrt[3]{r}\exp \bigl( i ( \tfrac13 \theta) \bigr), \\ \sqrt[3]{r}\exp \bigl( i ( \tfrac13 \theta %2B \tfrac23 \pi ) \bigr), \\ \sqrt[3]{r}\exp \bigl( i ( \tfrac13 \theta - \tfrac23 \pi ) \bigr). \end{cases}](/2012-wikipedia_en_all_nopic_01_2012/I/ec2289749728b6121b3ddc474a59abae.png)
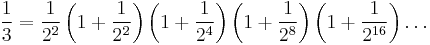
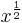
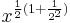
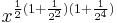
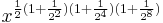
![x_{i%2B1} = \tfrac{4}{3}\sqrt[4]{a x_{i}} - \tfrac{1}{3}x_i.](/2012-wikipedia_en_all_nopic_01_2012/I/ee614b3f704306b3ce845ee6df8ae5b5.png)
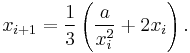
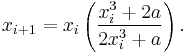
![\sqrt[3]{z} = \sqrt[3]{x^3%2By} = x%2B\cfrac{y} {3x^2%2B\cfrac{2y} {2x%2B\cfrac{4y} {9x^2%2B\cfrac{5y} {2x%2B\cfrac{7y} {15x^2%2B\cfrac{8y} {2x%2B\ddots}}}}}}](/2012-wikipedia_en_all_nopic_01_2012/I/8a0f3c90b7bcee42d529573649385e09.png)
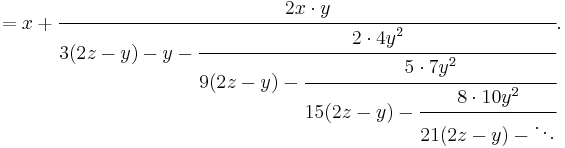
![\sqrt[3]{1} = 1](/2012-wikipedia_en_all_nopic_01_2012/I/d53d30c7123945d21786c0fb38eeeb18.png)
![\sqrt[3]{2} \approx1.259 \; 921 \; 049 \; 894 \; 873 \; 164 \; 767 \; 210](/2012-wikipedia_en_all_nopic_01_2012/I/289378d268f8e64a7234cc2c1f313df9.png)
![\sqrt[3]{3} \approx1.442 \; 249 \; 570 \; 307 \; 408 \; 382 \; 321 \; 638](/2012-wikipedia_en_all_nopic_01_2012/I/417e0270ed7da14a9a3419ec2c924c14.png)
![\sqrt[3]{4} \approx1.587 \; 401 \; 051 \; 968 \; 199 \; 474 \; 751 \; 705](/2012-wikipedia_en_all_nopic_01_2012/I/03cd27f2aaee5ab37dfdf3ae92dc3d24.png)
![\sqrt[3]{5} \approx1.709 \; 975 \; 946 \; 676 \; 696 \; 989 \; 353 \; 108](/2012-wikipedia_en_all_nopic_01_2012/I/982899e6a3a4fa15d7c44927185b1911.png)
![\sqrt[3]{6} \approx1.817 \; 120 \; 592 \; 832 \; 139 \; 658 \; 891 \; 211](/2012-wikipedia_en_all_nopic_01_2012/I/afe8a28aee9a4a96e8880a561a6a7335.png)
![\sqrt[3]{7} \approx1.912 \; 931 \; 182 \; 772 \; 389 \; 101 \; 199 \; 116](/2012-wikipedia_en_all_nopic_01_2012/I/b767c31d944e4c0fa8a8be9b20cd9855.png)
![\sqrt[3]{8} = 2](/2012-wikipedia_en_all_nopic_01_2012/I/268cbbda2dd912ea7e14c0527757ad39.png)
![\sqrt[3]{9} \approx2.080 \; 083 \; 823 \; 051 \; 904 \; 114 \; 530 \; 056](/2012-wikipedia_en_all_nopic_01_2012/I/7460670663a20f04092b346cdf372767.png)
![\sqrt[3]{10} \approx2.154 \; 434 \; 690 \; 031 \; 883 \; 721 \; 759 \; 293](/2012-wikipedia_en_all_nopic_01_2012/I/c35b378ec20c31e02b77af26a52d0143.png)
![\sqrt[3]{11} \approx2.223 \; 980 \; 090 \; 569 \; 315 \; 521 \; 165 \; 363](/2012-wikipedia_en_all_nopic_01_2012/I/5b1ed26a8150b8a74d2c643490b5a572.png)
![\sqrt[3]{12} \approx2.289 \; 428 \; 485 \; 106 \; 663 \; 735 \; 616 \; 084](/2012-wikipedia_en_all_nopic_01_2012/I/0f03409f96c8a627d2d17631e13d1444.png)
![\sqrt[3]{13} \approx2.351 \; 334 \; 687 \; 720 \; 757 \; 489 \; 500 \; 016](/2012-wikipedia_en_all_nopic_01_2012/I/68a4475966b810ead24a09dddc20b463.png)
![\sqrt[3]{14} \approx2.410 \; 142 \; 264 \; 175 \; 229 \; 986 \; 128 \; 369](/2012-wikipedia_en_all_nopic_01_2012/I/25edaed6a4a6bac7e820985ef1b7f5bf.png)
![\sqrt[3]{15} \approx2.466 \; 212 \; 074 \; 330 \; 470 \; 101 \; 491 \; 611](/2012-wikipedia_en_all_nopic_01_2012/I/93fe98b2d6d72c3190c0b678450c3a89.png)
![\sqrt[3]{16} \approx2.519 \; 842 \; 099 \; 789 \; 746 \; 329 \; 534 \; 421](/2012-wikipedia_en_all_nopic_01_2012/I/fb1110f8dadda27b6a08602a7b02be1e.png)
![\sqrt[3]{17} \approx2.571 \; 281 \; 590 \; 658 \; 235 \; 355 \; 453 \; 187](/2012-wikipedia_en_all_nopic_01_2012/I/c4eaa77150223090c1dc9225a8d6b481.png)
![\sqrt[3]{18} \approx2.620 \; 741 \; 394 \; 208 \; 896 \; 607 \; 141 \; 661](/2012-wikipedia_en_all_nopic_01_2012/I/b352c782fa3ee803c51c7c764281082a.png)
![\sqrt[3]{19} \approx2.668 \; 401 \; 648 \; 721 \; 944 \; 867 \; 339 \; 627](/2012-wikipedia_en_all_nopic_01_2012/I/43397e6cb1370c63e5e3b96de25ac1ae.png)
![\sqrt[3]{20} \approx2.714 \; 417 \; 616 \; 594 \; 906 \; 571 \; 518 \; 089](/2012-wikipedia_en_all_nopic_01_2012/I/43883ac5be32c4c75ec93b13857048c3.png)
![\sqrt[3]{21} \approx2.758 \; 924 \; 176 \; 381 \; 120 \; 669 \; 465 \; 791](/2012-wikipedia_en_all_nopic_01_2012/I/aaf369c5ec2683b4ad9592f60da42e06.png)
![\sqrt[3]{22} \approx2.802 \; 039 \; 330 \; 655 \; 387 \; 120 \; 665 \; 677](/2012-wikipedia_en_all_nopic_01_2012/I/6221c3e1059ad732dc377fcfd0eb0358.png)
![\sqrt[3]{23} \approx2.843 \; 866 \; 979 \; 851 \; 565 \; 477 \; 695 \; 439](/2012-wikipedia_en_all_nopic_01_2012/I/c2c619004be9305610be4de25dae64e3.png)
![\sqrt[3]{24} \approx2.884 \; 499 \; 140 \; 614 \; 816 \; 764 \; 643 \; 276](/2012-wikipedia_en_all_nopic_01_2012/I/417704ccd03e1a291221172611149cde.png)
![\sqrt[3]{25} \approx2.924 \; 017 \; 738 \; 212 \; 866 \; 065 \; 506 \; 787](/2012-wikipedia_en_all_nopic_01_2012/I/1a2d1225546c9b84d7efe15165126418.png)
![\sqrt[3]{26} \approx2.962 \; 496 \; 068 \; 407 \; 370 \; 508 \; 673 \; 062](/2012-wikipedia_en_all_nopic_01_2012/I/7bcded25e7cb4ef249f29f799cde9bf2.png)
![\sqrt[3]{27} = 3](/2012-wikipedia_en_all_nopic_01_2012/I/67381ec8caec72f64b963dec502cd8e0.png)